Теория вероятностей

Источник материала (opens in a new tab)

Что такое теория вероятностей

Теория вероятностей — это раздел математики, который позволяет нам анализировать события и предсказывать их логически обоснованным образом. Например, она помогает предсказывать погоду или оценивать риски в бизнесе. Эту теорию используют в разных сферах, таких как страхование, IT, сельское хозяйство, азартные игры и даже психология.

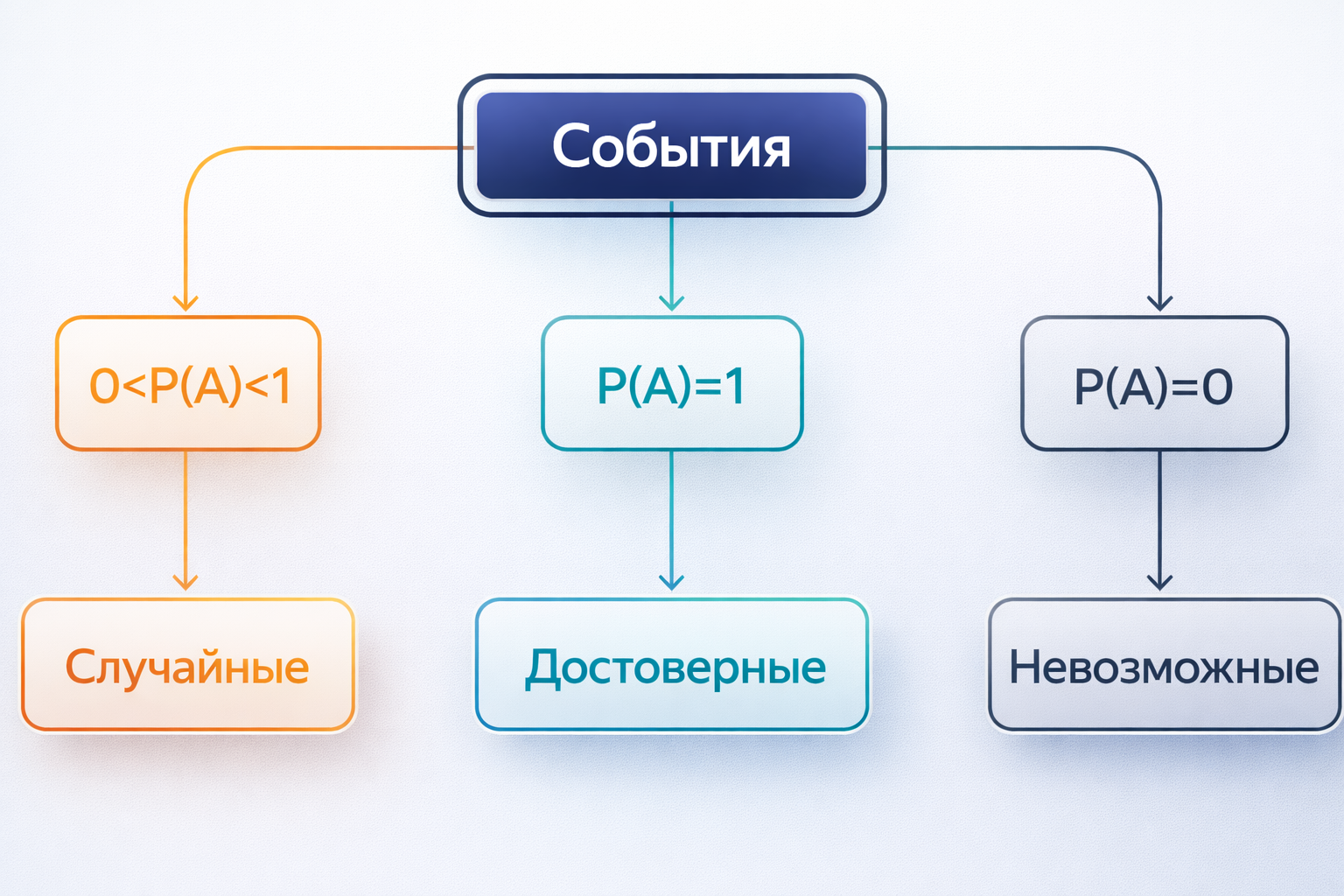
Вероятность события отражается в виде числа, которое всегда находится в диапазоне от нуля до единицы: ноль указывает, что событие не произойдёт, а единица — что оно точно произойдёт. Любое событие с вероятностью 1 считается достоверным, с 0 — невозможным, с вероятностью от 0 до 1 — случайным. Вероятности могут быть выражены в дробях, десятичных дробях или процентах. Например, если событие имеет вероятность ½ — это то же самое, что 0,5 или 50%.

Базовые определения

• Случайный эксперимент — повторяемое действие с непредсказуемым исходом (подброс кубика).
• Исход — конкретный результат эксперимента; все исходы образуют пространство исходов.
• Событие — подмножество исходов, удовлетворяющее условию.
• Вероятность — числовая оценка шанса события: при равновероятных исходах P(A) = m / n, где m — благоприятные, n — все исходы.

P(A) = m / n               # классическая вероятность (равновероятные исходы)
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)   # сумма совместных событий
P(A ∩ B) = P(A) * P(B)              # если A и B независимы
P(A | B) = P(A ∩ B) / P(B)          # условная вероятность
P(A^c) = 1 - P(A)                   # противоположное событие

Виды событий

• Противоположные: исключают друг друга, P(A) + P(A^c) = 1 (орёл vs не орёл).
• Несовместные: не могут произойти вместе; P(A ∪ B) = P(A) + P(B), если A и B несовместны.
• Совместные: могут произойти одновременно; P(A ∪ B) = P(A) + P(B) - P(A ∩ B).
• Независимые: одно не влияет на другое; P(A ∩ B) = P(A) * P(B).
• Зависимые: вероятность одного меняется при наступлении другого; P(A ∩ B) = P(A) * P(B | A).
• Условная вероятность: шанс A при условии B — P(A | B) = P(A ∩ B) / P(B).
• Байес: P(A | B) = P(B | A) * P(A) / P(B) — «переворачивает» условные вероятности.

Как решать задачи

1. Определить тип событий (совместные/несовместные, зависимые/независимые).
2. Выписать известные вероятности и формулы.
3. Подставить числа и посчитать.

Примеры расчётов

1. Два туза подряд без возврата
Колода 52 карты, тузов 4.
P(первый туз) = 4/52, P(второй туз | первый туз) = 3/51.
P(два туза) = 4/52 * 3/51 ≈ 0.5%.

2. Чёрная карта или шестёрка
P(шестёрка)=4/52, P(чёрная)=26/52, совместное P(чёрная шестёрка)=2/52.
P(чёрная ∪ шестёрка) = 4/52 + 26/52 - 2/52 = 28/52 ≈ 0.54.

3. Условная вероятность (естествознание при условии математики)
P(математика и естество)=0.4, P(математика)=0.6.
P(естество | математика) = 0.4 / 0.6 ≈ 0.67.

4. Байес: болезнь сердца при условии курения
P(болезнь)=0.1, P(курит)=0.05, P(курит | болезнь)=0.07.
P(болезнь | курит) = 0.07 * 0.1 / 0.05 = 0.14 (14%).

Самопроверка

Задача 1. Есть пять зелёных и семь красных шаров. Два шара выбираются по одному без замены. Найти вероятность того, что первый шар будет зелёным, а второй — красным.

P(A) = 5/12
P(B | A) = 7/11
P(A ∩ B) = (5/12) * (7/11) = 35/132 ≈ 0.265

Задача 2. В колоде 52 карты — по 13 карт каждой масти (черви, бубны, трефы, пики). Найти вероятность того, что не выпадет карта червовой масти.

P(черви) = 13/52 = 1/4
P(¬черви) = 1 - 1/4 = 3/4

Задача 3. У игрального кубика шесть граней. Нужно вычислить вероятность того, что не выпадет грань с единицей.

P(1) = 1/6
P(¬1) = 1 - 1/6 = 5/6

Дополнительно

Примеры задач по теории вероятности (opens in a new tab)

Теория вероятностей. Базовые термины и понятия (opens in a new tab)